网络流学习笔记(好像是 ckj 写的)
[編輯] [转简体] (简体译文)概要
正文
Part 1 什么是网络流
1.概念
网络可以理解为一堆水管,而流则可以理解为水流。水流可以从源头源源不断地流进管道系统,然后从排水口流出管道系统。
但因为水管是有大小的,如果单位时间流过的水比这跟水管的容量还大,那么这跟水管就会被撑爆。所以,单位时间内每根水管能流的水量是有限的,我们把第 $i$ 根水管的容量记为 $ci$,表示第 $i$ 根水管在单位时间内最多能流 $ci$ 那么多的水。
而且由于水往低处流,所以水管是有方向的。
管道系统肯定不止一根水管,而多根水管连起来就需要一些节点。我们可以把节点理解为水流中继站,因为水流中继站肯定不会把水给吞了,所以流入某个中继站的水流总量和流出这个中继站的水流总量是相等的。
把这个水管系统画出来大概就是这样的:(S 表示源头,T 表示排水口,箭头表示水管,箭头旁边的数字表示水管的容量)
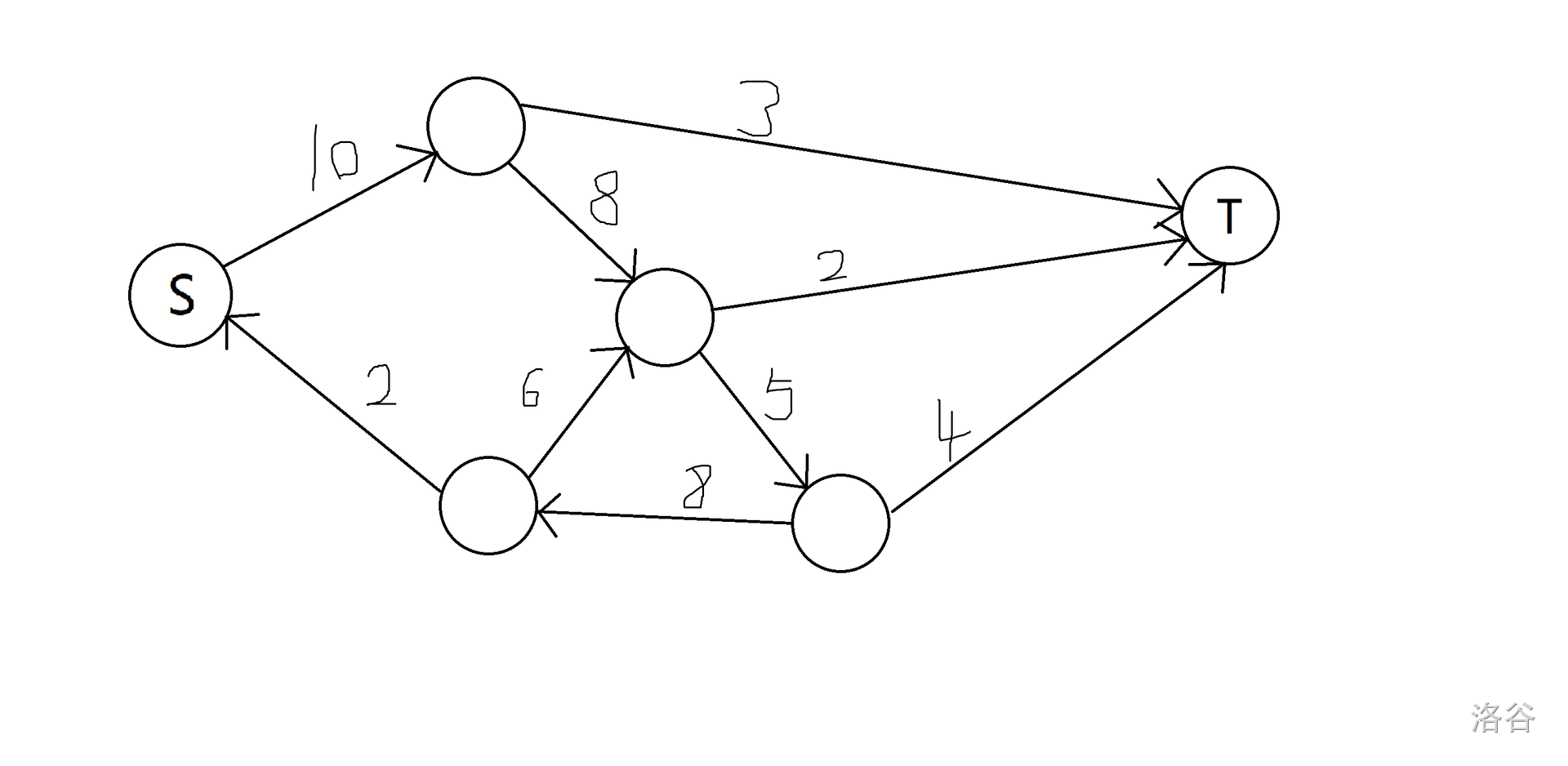
在上图中,我们发现其实源头和排水口也可以当成中继站来用。
这种图是不是很眼熟?没错!这是一个带权有向图,水管在图里是边,水管的容量是边权,中继站是节点,源头和排水口也是节点。
2.术语
因为像 水管容量、排水口出水量、水管系统 这类名字众 Oier 不喜欢,所以大家给它们取了一些~~听起来很高级~~学术化的名字。
大家把 水管 叫做边,水管容量 叫做边的容量,排水口出水量 叫做流量,水管系统 叫做网络,源头 叫做源点,排水口 叫做汇点,中继站 叫做节点。
也就是
#define 边 水管 #define 边的容量 水管容量 #define 流量 排水口出水量 #define 网络 水管系统 #define 源点 源头 #define 汇点 排水口 #define 节点 中继站
Part 2 网络最大流问题
1.定义
顾名思义,“网络最大流” 即一个网络在单位时间内最多能流多少流量。而网络最大流问题即给你一个网络和源点、汇点编号,要你求这个网络的最大流。
举个例子,对于下图中的网络,它的最大流便为 10。

2.求解
如何用算法求解网络最大流呢?
考虑最~~暴力~~朴素的做法,很显然可以爆搜,但时间复杂度会爆炸的。
现在有请我们的嘉宾——猴子,来帮忙求解网络最大流。
### 反向边的引入
我们给猴子一个这样的网络(边上的数表示这条还有多少容量)
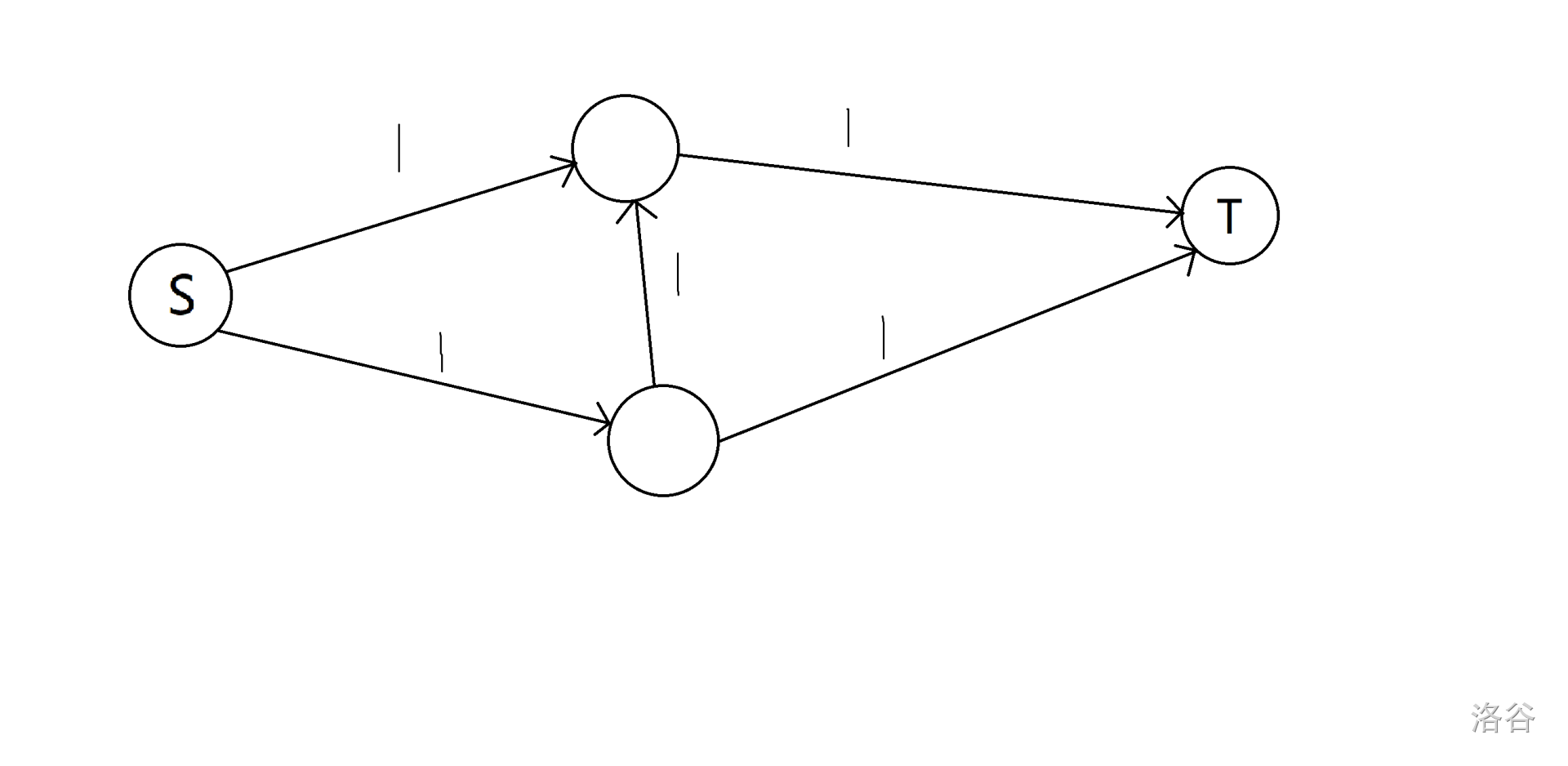
猴子很开心,因为它一眼就看见了一条可以让流 1 流量的路
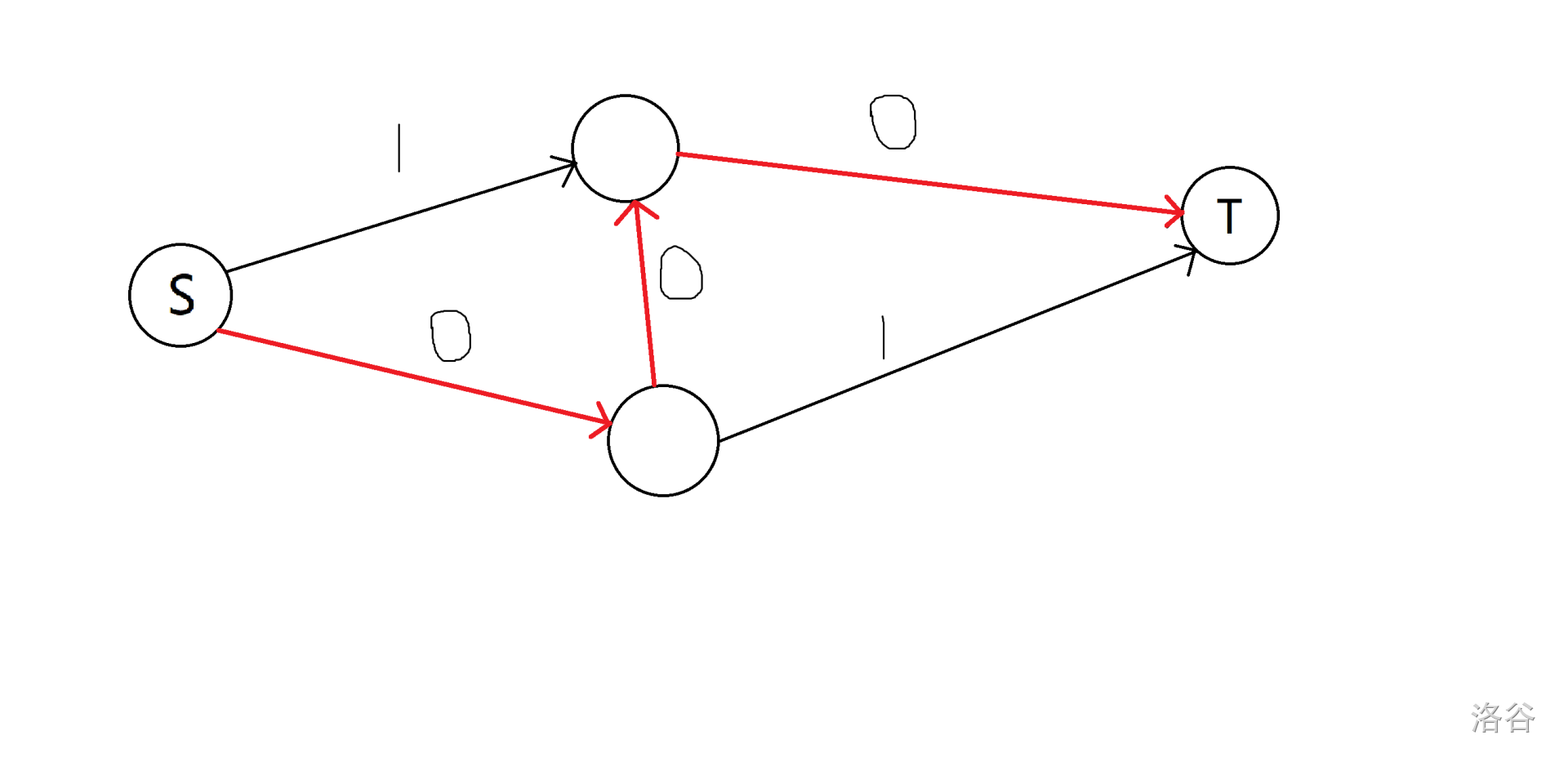
现在这个网络的最大流从原来的 0 更新成了 1。
猴子尝试继续找路,可它发现找不到路了,于是猴子跑路了。
Oier 们又来搞事情了,大家觉得 路 不好听,所以把猴子找的这种路叫做增广路。
那么猴子求出来的是最大流吗?不,很明显可以让上面的两条边通过 1 的流量,再让下面的两条边通过 1 的流量,整个网络的最大流其实是 2 而不是 1。
猴子被友好的工作人员请回来了,现在它开始反思,为什么它会错呢?114514 秒过去了,猴子终于知道自己错误的原因了,那就是它不会反悔。如果能不经过中间那条边它求的最大流就会变成 2 了。
猴子跑去吃香蕉了,我们又要自己思考做法了。
吸取了猴子惨痛的失败经验后,我们发现,电脑其实也像一只猴子,它并不会反悔。那如何教会电脑反悔呢?建反向边就行啦!
不过要注意,反向边的容量一开始是 0。
例如我们之前给猴子的网络,建完反向边之后就变成这样了
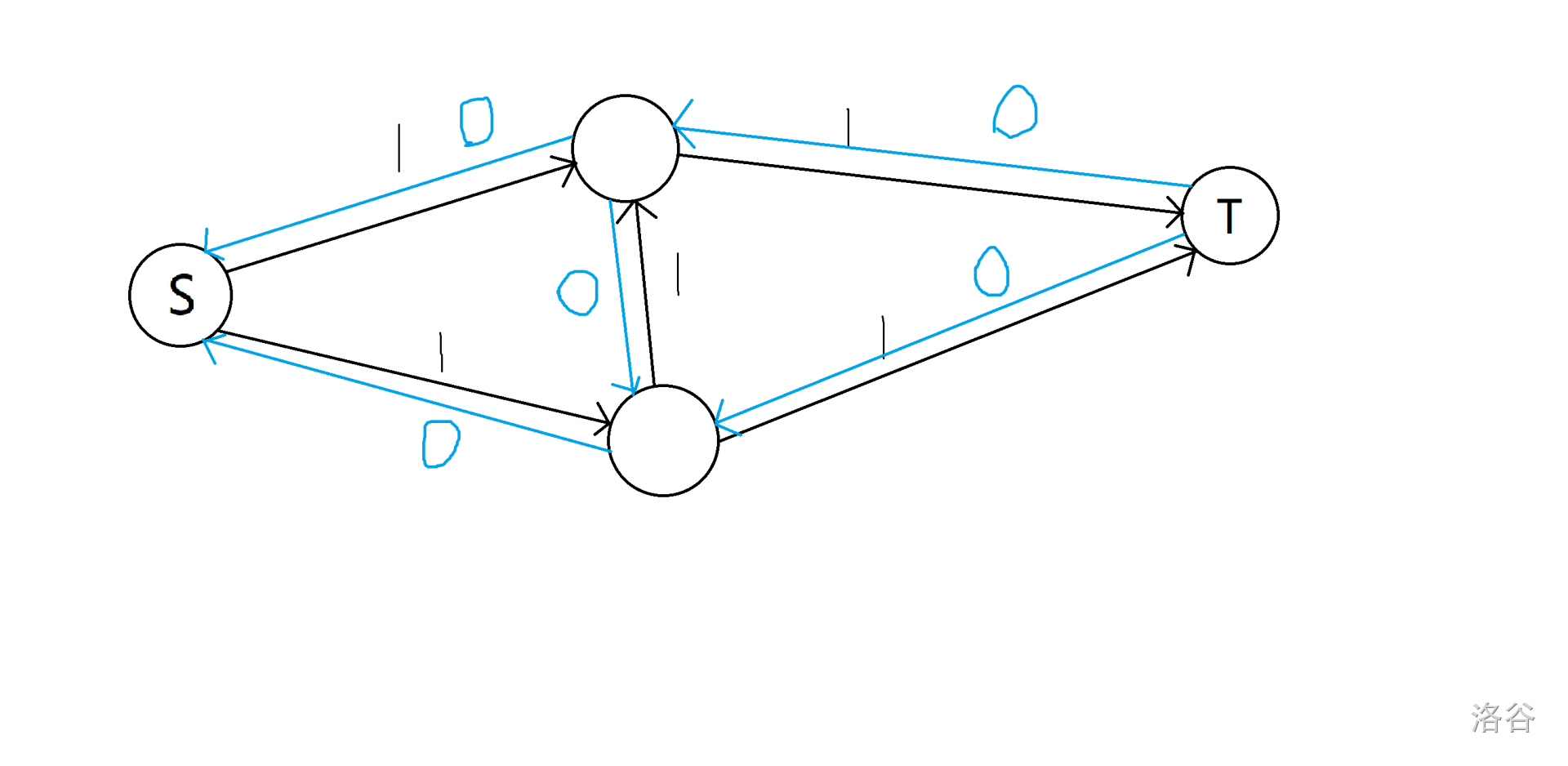
反向边如何使用呢?很简单,当一条边流过 $k$ 的流量时,反向边便增加 $k$ 的容量;当一条边的反向边流过 $k$ 的流量时,它的正向边便增加 $k$ 的容量。这样相当于给了电脑一个反悔的机会,如果这条边流过去了 $k$ 的流量,那么它的反向边流 $k$ 的流量就相当于把流走的流量还给流量流出去的节点。
增加反向边后,猴子就会发现它能轻松地求出网络最大流了。
首先,猴子还是找到了之前那一条增广路。不过这次它把反向边的容量增加了
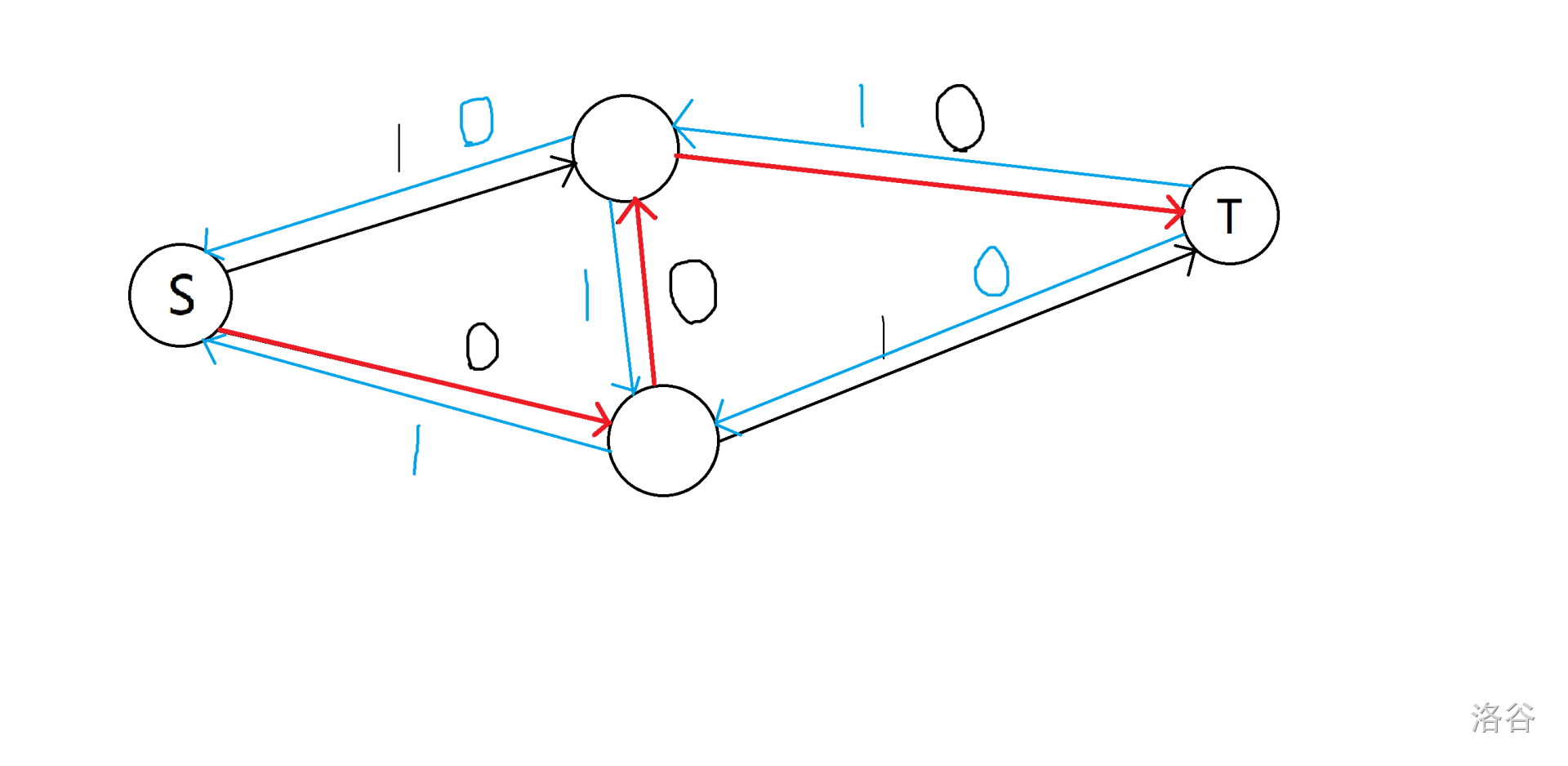
现在猴子发现它还能找增广路
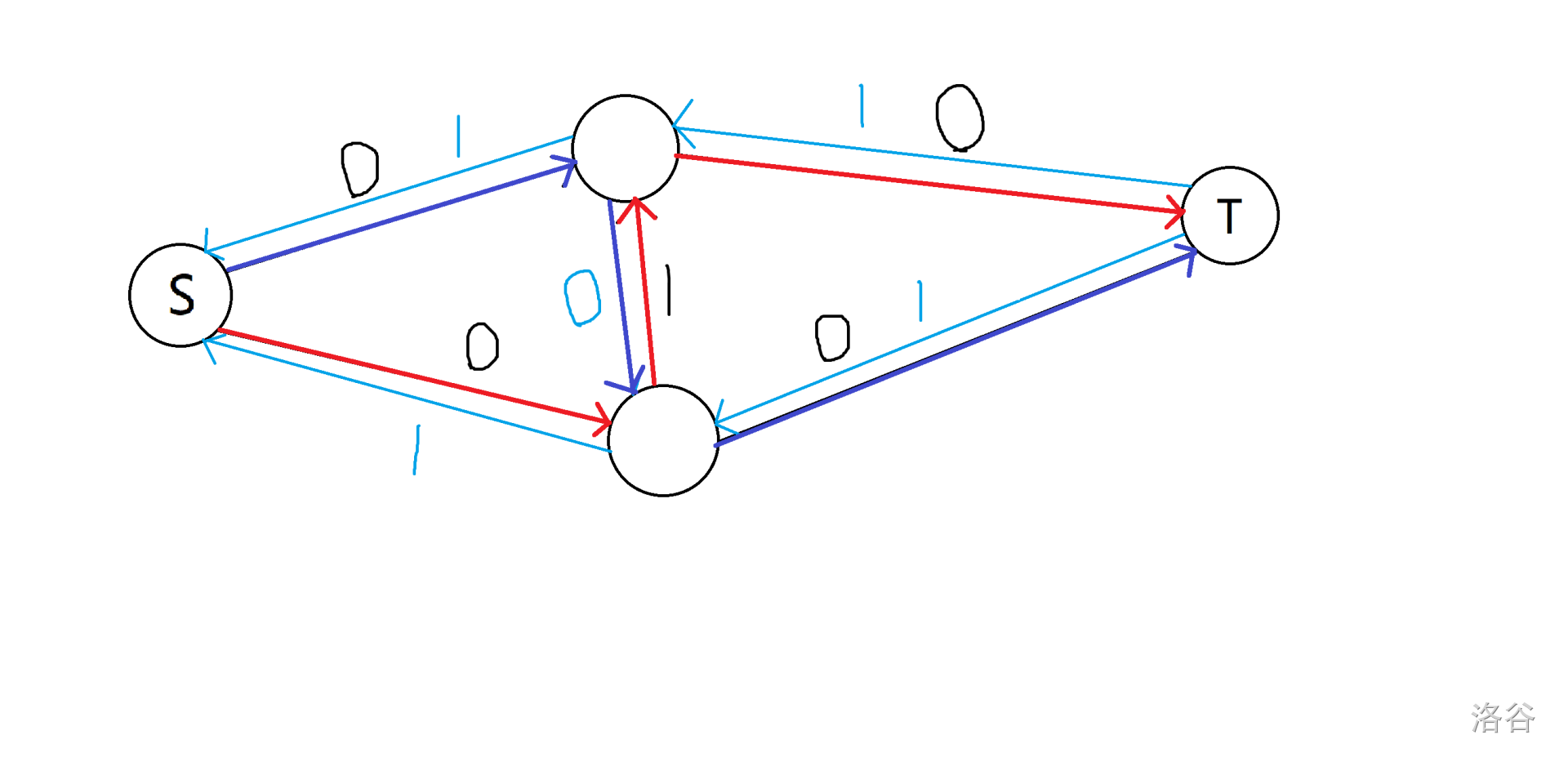
这下它总算求出了正确答案,猴子开心地跑了。
我们发现,猴子在找第二条增广路的时候走了中间那条边的反向边。这其实表示猴子反悔了,它让红色那条增广路不走中间那条边,改成走右下那一条,而当前的增广路 “接管” 了之前红色增广路走的边。
### EK 算法
有了反向边,电脑也可以轻松地求网络最大流了。
建完图后,我们可以用 bfs 来找增广路。根据网络最大流的定义,bfs 应该从源点开始,到汇点结束。所以如果 bfs 时访问到了汇点,那么电脑就找到了一条增广路。
找到增广路之后还得把增广路上的正向边的剩余容量减少,把反向边的剩余容量增加。所以我们需要一个数组 pre,$pre_i$ 表示在当前找到的增广路中,$i$ 是从哪一条边过来的。
特别的,反向边的存储有个特殊方式,那就是 $i$ 的反向边编号为 $i$ $xor$ $1$,写成代码就是 x^1。这么规定是因为电脑很笨,它在更新剩余容量的时候不知道哪一条是正向边,哪一条是反向边,所以我们需要 $xor$ 这种对称(雾)的操作。
例如: 2 号边的反向边就是 2^1=3,而 3 号边的反向边就是 3^1=2。
问题又来了,1^1=0,因为我们不喜欢 0 这个数字,所以边的编号应该从 2 开始,也就是一开始 esum=1(esum 表示当前边的条数)。
由于一个网络可能不止一条增广路,所以我们需要跑很多次 bfs,一直跑到找不到增广路为止。
这种利用很多次 bfs 来求网络最大流的算法被称为 EK 算法
。
附上 EK 算法的代码:
// P3376
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
typedef long long ll;
int n,m,s,t;
int esum,to[10005],head[205],nxt[10005];
ll ans,c[10005],f[10005];
int las[205];
bool vis[205];
inline void init()
{
esum=1;
memset(head,-1,sizeof(head));
}
inline void add(int x,int y,ll w)
{
c[++esum]=w;
to[esum]=y;
nxt[esum]=head[x];
head[x]=esum;
}
inline bool bfs()
{
queue<int> q;
q.push(s);
memset(vis,0,sizeof(vis));
vis[s]=true;
f[s]=1e17;
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=head[u];i!=-1;i=nxt[i])
{
int v=to[i];
if(c[i]>0&&!vis[v])
{
las[v]=i;
f[v]=min(f[u],c[i]);
vis[v]=true;
q.push(v);
if(v==t)
{
return true;
}
}
}
}
return false;
}
inline ll upd()
{
ll nflow=0;
nflow+=f[t];
int u=t;
while(u!=s)
{
int i=las[u];
c[i]-=f[t];
c[i^1]+=f[t];
u=to[i^1];
}
return nflow;
}
inline ll ek()
{
ll maxflow=0;
while(bfs())
{
maxflow+=upd();
}
return maxflow;
}
int main()
{
scanf("%d%d%d%d",&n,&m,&s,&t);
init();
for(int i=1;i<=m;i++)
{
int x,y;
ll w;
scanf("%d%d%lld",&x,&y,&w);
add(x,y,w);
add(y,x,0);
}
printf("%lld\n",ek());
return 0;
}### dinic 算法
在 EK 算法中,我们需要跑很多次 bfs 才能得到答案。但 bfs 在最坏情况下是要访问所有节点的,这导致 EK 算法的时间复杂度并不够优秀。所以,人们发明了 dinic 算法。
dinic 算法是一种十分巧妙的算法,它利用了层次图来减少 bfs执行的次数。
#### 层次图
层次图,顾名思义,就是把图分层。可以这么理解:一张图本来是平的,现在有个人把它放在了山坡上,它就斜过来了。由于水往低处流,所以把一个网络分层之后,水流(流)就只能从高处(深度小)的节点流向低处(深度大)的节点,而分层的过程其实就是一次 bfs。
分层的流程大概如下:首先把源点的深度设置成 1,然后访问和源点相连的其它点,把它们的深度设置成 2,依此类推。
#### 算法流程
首先我们需要把网络分层,然后对于分完层的网络,我们再跑很多遍 dfs。但是在 dfs里我们只允许当前节点的流向深度正好比当前节点深度大 1 的节点流去。这样保证了 dinic 算法的正确性,其实也可以理解为用 dfs 来跑 EK 算法中的 bfs。但是用 dfs 有个好处,那就是 bfs 需要遍历完整个图才能找到一条增广路,而 dfs 遍历整个图有可能会找到多条增广路。
如果 dfs 到达不了汇点了(找不到增广路了),那么就需要重新分层,再跑一次 bfs。如果 bfs 到达不了汇点,那么就说明增广路找完了,求出了网络最大流。
写成伪代码大概是这样的:
dfs 部分:
dfs(int u,int w) // u 表示当前节点的编号,w 表示流向当前点的流量
{
遍历所有从 u 出发的边 i
{
int v=i 到达的节点;
if(v 的深度 == u 的深度 +1)
{
int re=dfs(v,min(w,i 的容量));
if(增广成功)
{
更新正向边和反向边的容量;
return re;
}
}
}
return 增广失败;
}求解部分:
while(bfs 可以到达 汇点)
{
while(增广路增广的流量 = dfs(s,inf) != 增广失败)
{
网络最大流+=增广路增广的流量;
}
}此外,dinic 算法还有两个优化,分别是多路增广优化和当前弧优化。多路增广优化就是令一次 dfs 能够找到多条增广路,而当前弧优化就是令 dfs 不再增广增广过的边。
附上没加优化的代码和加了这两个优化的代码:
没加优化的:
// P3376
#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
typedef long long ll;
int n,m,s,t;
int esum,to[10005],nxt[10005],h[205];
ll c[10005];
int dep[205];
inline void init()
{
esum=1;
memset(h,-1,sizeof(h));
}
inline void add(int x,int y,ll w)
{
c[++esum]=w;
to[esum]=y;
nxt[esum]=h[x];
h[x]=esum;
}
inline bool bfs()
{
memset(dep,0,sizeof(dep));
queue<int> q;
q.push(s);
dep[s]=1;
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=h[u];i!=-1;i=nxt[i])
{
int v=to[i];
if(c[i]>0&&dep[v]==0)
{
dep[v]=dep[u]+1;
q.push(v);
}
}
}
return dep[t]!=0;
}
ll dfs(int u,ll w)
{
if(u==t)
{
return w;
}
for(int i=h[u];i!=-1;i=nxt[i])
{
int v=to[i];
if(c[i]>0&&dep[v]==dep[u]+1)
{
ll re=dfs(v,min(w,c[i]));
if(re>0)
{
c[i]-=re;
c[i^1]+=re;
return re;
}
}
}
return 0;
}
inline ll dinic()
{
ll ans=0;
while(bfs())
{
while(ll tmp=dfs(s,1e18))
{
ans+=tmp;
}
}
return ans;
}
int main()
{
init();
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;i++)
{
int x,y;
ll w;
scanf("%d%d%lld",&x,&y,&w);
add(x,y,w);
add(y,x,0);
}
printf("%lld\n",dinic());
return 0;
}加了两个优化的:
// P3376
#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
typedef long long ll;
int n,m,s,t;
int esum,to[10005],nxt[10005],h[205];
ll c[10005];
int dep[205],cur[205];
inline void init()
{
esum=1;
memset(h,-1,sizeof(h));
}
inline void add(int x,int y,ll w)
{
c[++esum]=w;
to[esum]=y;
nxt[esum]=h[x];
h[x]=esum;
}
inline bool bfs()
{
memset(dep,0,sizeof(dep));
queue<int> q;
q.push(s);
dep[s]=1;
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=h[u];i!=-1;i=nxt[i])
{
int v=to[i];
if(c[i]>0&&dep[v]==0)
{
dep[v]=dep[u]+1;
q.push(v);
}
}
}
return dep[t]!=0;
}
ll dfs(int u,ll w)
{
if(u==t)
{
return w;
}
ll sum=0;
for(int i=cur[u];i!=-1;i=nxt[i],cur[u]=nxt[cur[u]])
{
int v=to[i];
if(c[i]>0&&dep[v]==dep[u]+1)
{
ll re=dfs(v,min(w,c[i]));
c[i]-=re;
c[i^1]+=re;
sum+=re;
w-=re;
if(w==0)
{
break;
}
}
}
return sum;
}
inline ll dinic()
{
ll ans=0;
while(bfs())
{
for(int i=1;i<=n;i++)
{
cur[i]=h[i];
}
ans+=dfs(s,1e18);
}
return ans;
}
int main()
{
init();
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;i++)
{
int x,y;
ll w;
scanf("%d%d%lld",&x,&y,&w);
add(x,y,w);
add(y,x,0);
}
printf("%lld\n",dinic());
return 0;
}