問題概述

現有兩個矩形，假設其中一個固定不動（rctMain），另一個可以移動（rctSub），它們如果存在重疊部分，則需要將 rctSub 移出 rctMain。

算法介紹

此算法分兩步。

1. 判斷上述兩矩形是否相交
   

2. 確定如何移出重疊的矩形

1. 判斷兩矩形是否相交

錯誤方案 1（頂點判據）

判斷 rctSub 的四個頂點是否在 rctMain 中，若有任一頂點在其中則認爲 rctMain 與 rctSub 相交，否則不交。

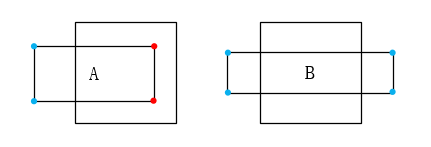
此方案錯誤，因爲相交的矩形不一定具有頂點的包含關係。如下圖，按照此方案，A 情況判斷正確，但 B 情況判斷錯誤。

錯誤方案 2（邊判據）

將 rctSub 的上下左右四條邊分別和 rctMain 中與之平行的兩條邊進行座標比較，例如 

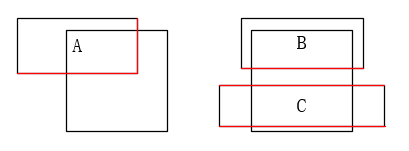
if (rctMain.left < rctSub.left && rctSub.left < rctMain.right)
{
    // 認爲 rctSub.left 在 rctMain 內部
}

其餘三條邊以此類推。由此可以得到 rctSub 的上下左右四條邊陷入 rctMain 的情況，據此判斷 rctSub 和 rctMain 的重疊情況，如下圖：

對於 A，可以判斷出其右下兩條邊陷入 rctMain，因此確定相交，且可以考慮往左上移出；

對於 B，可以判斷出其下邊陷入 rctMain，因此確定相交，可以考慮向上移出；

對於 C，可以判斷出其上下兩條邊都陷入 rctMain，因此確定相交，但還需要進一步計算確定如何移出。

完整代碼如下：

// 標記 rctSub 的哪條邊陷入 rctMain 中
bool bT = false;
bool bB = false;
bool bL = false;
bool bR = false;

int t0 = rctMain.t();
int b0 = rctMain.b();
int l0 = rctMain.l();
int r0 = rctMain.r();

int t = rctSub.t();
int b = rctSub.b();
int l = rctSub.l();
int r = rctSub.r();

// 判定陷入時，只進行平行邊之間的判斷
if (t0 < t && t < b0) { bT = true; }
if (t0 < b && b < b0) { bB = true; }
if (l0 < l && l < r0) { bL = true; }
if (l0 < r && r < r0) { bR = true; }

// 無需修正的情況（任意一組文本平行邊完全沒有陷入，即說明文本與檢測箱相離）
if ((!bT && !bB) || (!bL && !bR))
    return;

// 完全陷入的情況
if (bT && bB && bL && bR)
    return;    // TODO ...

// 同一組平行邊都陷入時，不能作爲修正依據（因爲無法確定這個方向上如何移動）
if (bT && bB) {}
else if (bT) { rctTxt.alignT(b0); }
else if (bB) { rctTxt.alignB(t0); }

if (bL && bR) {}
else if (bL) { rctTxt.alignL(r0); }
else if (bR) { rctTxt.alignR(l0); }

此方案也錯誤，因爲只將 rctSub 的上下左右四條邊分別和 rctMain 中與之平行的兩條邊進行座標比較，相當於是忽略了另一個方向上的信息。例如，對於下面的情況將得出錯誤的結論：

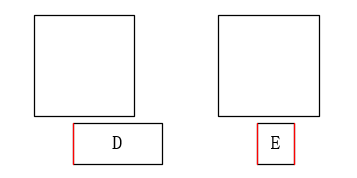
對於 D，將被誤判爲左邊陷入 rctMain，導致被判定爲相交，且將被向右移出；

對於 E，將被誤判爲左右兩邊都陷入 rctMain，導致被判定爲相交。

這個方案在判斷相交時只在兩個矩形的平行邊之間進行座標比較，而忽略了矩形是二維形狀，必須同時研究其 x 和 y 兩個方向的邊界。此方案相當於是把矩形當成了下面的這種十字架圖形：

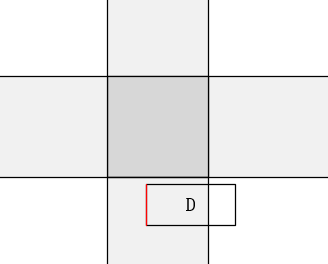
因此此方案亦不可取。

正確方案

直接計算出兩矩形的交集，若爲空集即表示不相交，否則表示相交。

在計算時，將矩形正交分解到 x, y 兩個方向分別取交集，如果結果都不是空集，即說明兩矩形相交，否則不相交。

代碼將在後面一併給出。

2. 確定如何移出 rctSub

在確定 rctSub 與 rctMain 相交後，需要將 rctSub 移出 rctMain。我們並不需要同時在 x 和 y 方向移動 rctSub，因爲在一個方向移動就可以將其移出 rctMain，倘若在兩個方向同時移動，則 rctSub 將總是和 rctMain 共一個頂點，這不是我想要的效果。

爲了確定究竟往哪個方向將 rctSub 移出 rctMain，我採用了如下公式進行計算。

記 分別表示 rctSub 和 rctMain 在 x 和 y 方向上的交集（閉區間），則有：

上面公式中，區間的 .left 和 .right 表示區間的左右端點。

只要 rctSub 與 rctMain 相交，那麼 必然非空，並且是 rctMain 在相應方向上投影區間的子集，因此上式中 的絕對值都小於 1，它們的絕對值代表在相應方向上移出 rctSub 的趨勢大小，而它們的正負指明了應該往相應方向的正方向還是負方向移出 rctSub（正即表示應從正方向移出，負即表示應從負方向移出）。因此我們只需要比較 的絕對值哪個大，就可以確定要從哪個方向移出 rctSub。

參考代碼

以下是參考代碼，是我在 BSch3V 項目中寫的，因此用的是此項目的矩形類型 SRect，但它和一般的 RECT 類型區別並不大。

rectoperation.h

/****************************************************************************
    BSch3V schematic capture
    Copyright (C) 1997-2014 H.Okada

    此文件爲匯東增入，用於處理矩形位置相關問題

*****************************************************************************/

#ifndef RECTOPERATION_H
#define RECTOPERATION_H

#include "coord.h"    // 提供 SRect


// 對重疊的矩形進行位置修正
void CorrectOverlappingRect(const SRect& rctMain, SRect& rctSub);

// 將相離的兩個矩形吸附在一起
void AdsorbRect(const SRect& rctBox, SRect& rctTxt);

#endif

rectoperation.cpp

#include "stdafx.h"
#include "rectoperation.h"

//（閉）區間
struct Range
{
    int left;
    int right;

    // 判斷此區間是否爲空
    bool IsEmpty() const
    {
        return right < left;
    }

    // 獲取區間長度
    int Length() const
    {
        return right - left;
    }
};

// 獲取相交區間（可能返回 right 小於 left 的區間，即表示空區間）
Range GetIntersectingRange(const Range& a, const Range& b)
{
    Range r = {
        max(a.left, b.left),
        min(a.right, b.right)
    };
    return r;
}

// 函數功能：
//   檢測兩個矩形是否發生相交
// 
// 參數說明：
//   [in]  rctA, rctB    待判定的矩形
//   [out] _rX, _rY        如果矩形的確相交，則傳出在 x, y 方向的相交區間
//
// 返回值：
//   返回 true 表示兩矩形相交，否則返回 false
//
bool checkIntersection(const SRect& rctA, const SRect& rctB, Range& _rX, Range& _rY)
{
    Range rX = GetIntersectingRange(
        { rctA.l(), rctA.r() },
        { rctB.l(), rctB.r() }
    );
    Range rY = GetIntersectingRange(
        { rctA.t(), rctA.b() },
        { rctB.t(), rctB.b() }
    );

    // 如果 rX 和 rY 都非空，則說明兩個矩形有交集
    if (!rX.IsEmpty() && !rY.IsEmpty())
    {
        _rX = rX;
        _rY = rY;
        return true;
    }
    else
    {
        return false;
    }
}

// 計算推力的標準向量
//
// 備註：
//   rMain 爲固定矩形正交分解的一個區間，rSub 爲其子集。
//   rSub 代表需要修正的矩形與固定矩形在某個方向（x / y）上的交集。
//   計算出的推力帶正負，絕對值小於 1，表示在該方向上將 rSub 推出 rMain 所用力量的大小。
//
double CalcForceStdVec(const Range& rMain, const Range& rSub)
{
    return (double)((rSub.left - rMain.left) + (rSub.right - rMain.right)) / rMain.Length();
}

// 函數功能：
//   對重疊的矩形進行位置修正
//
// 參數說明：
//   [in]      rctMain    固定矩形
//   [in, out] rctSub    待修正矩形
//
void CorrectOverlappingRect(const SRect& rctMain, SRect& rctSub)
{
    // 兩矩形相交的區間（正交分解後）
    Range rX, rY;

    // 若不相交，則不必修正
    if (!checkIntersection(rctMain, rctSub, rX, rY))
        return;

    // x, y 方向的標準推力（帶正負，絕對值小於 1）
    double vX = CalcForceStdVec({ rctMain.l(),rctMain.r() }, rX);
    double vY = CalcForceStdVec({ rctMain.t(),rctMain.b() }, rY);

    // 只需要在 x 或 y 一個方向修正矩形位置即可，此處哪個方向力大就選用哪個方向
    if (fabs(vX) > fabs(vY))
    {
        if(vX < 0) { rctSub.alignR(rctMain.l()); }    // 左推
        else { rctSub.alignL(rctMain.r()); }        // 右推
    }
    else
    {
        if (vY < 0) { rctSub.alignB(rctMain.t()); }    // 上推
        else { rctSub.alignT(rctMain.b()); }        // 下推
    }
}

// 函數功能：
//   將相離的兩個矩形吸附在一起
//
// 參數說明：
//   [in]      rctMain    固定矩形
//   [in, out] rctSub    待修正矩形
//
void AdsorbRect(const SRect& rctMain, SRect& rctSub)
{
    // 固定矩形位置
    int t0 = rctMain.t();
    int b0 = rctMain.b();
    int l0 = rctMain.l();
    int r0 = rctMain.r();

    // 待修正矩形位置
    int t = rctSub.t();
    int b = rctSub.b();
    int l = rctSub.l();
    int r = rctSub.r();

    // 磁性吸附
    if (t > b0) { rctSub.alignT(b0); }
    if (b < t0) { rctSub.alignB(t0); }
    if (l > r0) { rctSub.alignL(r0); }
    if (r < l0) { rctSub.alignR(l0); }
}